Lernaufgabe 5: Spule
Hier geht es zum Lernauftrag ohne Lösungen
Eingangsexperiment
Aufgebaut wird folgende Schaltung:
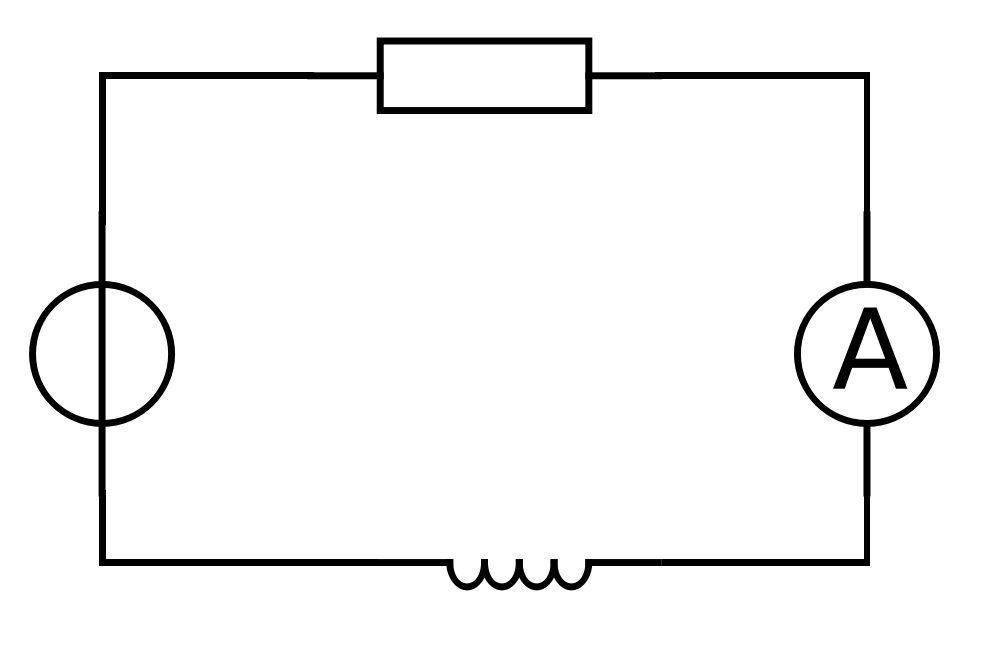
Die Spannungsquelle kann sowohl Gleich- als auch Wechselspannung liefern.
Versuch 1: Die Schaltung wird mit Gleichspannung versorgt und der Strom gemessen.
Versuch 2: Die Schaltung wird mit einer Wechselspannung gleicher Höhe versorgt und der Strom gemessen.
Bevor der Versuch durchgeführt wird entscheide dich für eine der folgenden Vermutungen:
1) Der Strom bei Gleichspannung ist geringer als bei Wechselspannung.
2) Die Höhe des Stroms bleibt gleich, egal ob Gleich- oder Wechselspannung.
3) Der Strom bei Gleichspannung ist höher als bei Wechselspannung.
Lösung
Vermutungen kriegen keine Musterlösung und werden am Ende des Lernauftrags nochmal zusammengefasst.
Arbeitsauftrag: Erarbeite das Verhalten einer Spule im Wechselstromkreis.
Material:
- https://www.leifiphysik.de/elektrizitaetslehre/elektromagnetische-induktion/versuche/selbstinduktion-qualitativ
- Fachbuch Kapitel 7.3.1: Induktiver Blindwiderstand
Im Verlauf der Erarbeitung beantworte die folgenden Aufgaben.
Aufgabe 1
Gib das Schaltzeichen einer Spule an.
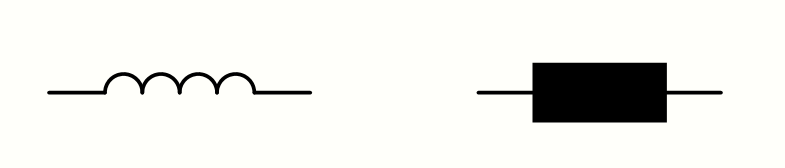
Aufgabe 2
Benenne die Ursache für die geringere Stromaufnahme einer Spule an Wechselspannung als bei Gleichspannung.
Lösung
Eine Änderung der Spannung führt zu verändertem Stromfluss durch die Spule, was zur Ausbildung eines Magnetfeldes in der Spule führt. Eine Änderung des Magnetfeldes in der Spule führt zur Induktion einer Spannung zwischen den Spulenenden, die sogenannte Selbstinduktion. Diese Selbstinduktion steht dem Stromfluss entgegen und verringert ihn.
Je schneller sich die Spannung ändert, desto größer ist der Effekt der Selbstinduktion und desto größer die Hemmung des Stroms durch die Spule.
Aufgabe 3
Vervollständige den folgenden Satz:
Eine Spule im Wechselstromkreis hat einen induktionen Blindwiderstand, der durch Spannungsänderung / Selbstinduktion entsteht.
Aufgabe 4
Innerhalb der Spule entsteht eine Selbstinduktionsspannung. Diese wirkt hemmend auf den Strom \(I\). Bei einer idealen Spule (Drahtwiderstand \(R=0\ \Omega\)) erreicht der Spulenstrom seinen
Scheitelwert jeweils eine Viertelperiode (\(90^\circ\)) später als die Spannung \(U_\mathrm{bL}\).
Vervollständige den Satz:
Im induktiven Blindwiderstand eilt der Wechselstrom der Wechselspannung um 90° nach.
Aufgabe 5
Trage den Strom- und Spannungszeiger (\(I\) und \(U_\mathrm{bL}\)) einer idealen Spule in das Zeigerbild ein.
Wenn ein Zeigerbild noch Neuland sein sollte, so recherchiere vorher, was ein Zeigerbild ist.
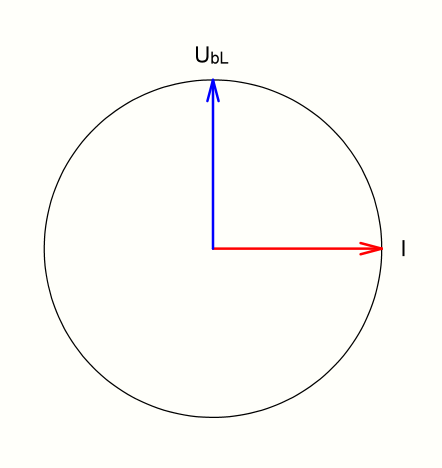
Aufgabe 6
Gib das Formelzeichen, die Einheit und die Formel zur Berechnung des induktiven Blindwiderstandes an.
Lösung
Formelzeichen \(X_L\)
Einheit: \(\Omega\)
Formel: \(X_L=\omega\cdot L=2\cdot\pi\cdot f\cdot L\)
Aufgabe 7
Die Induktivität \(L\) ist ein Maß für die Höhe der Selbstinduktionsspannung einer Spule. Auch die Frequenz \(f\) hat einen Einfluss auf den Blindwiderstand.
Trage in die folgende Tabelle die Wirkung auf den Blindwiderstand ein.
Lösung
| Veränderung | Wirkung auf \(X_L\) |
|---|---|
| Induktivität \(L\) \(\uparrow\) | \(\uparrow\) |
| Induktivität \(L\) \(\downarrow\) | \(\downarrow\) |
| Frequenz \(f\) \(\uparrow\) | \(\uparrow\) |
| Frequenz \(f\) \(\downarrow\) | \(\downarrow\) |
Aufgabe 8
Gib das Formelzeichen und die Einheit der Induktivität an.
Lösung
Formelzeichen: \(L\)
Einheit: \(H\) (Henry)
Aufgabe 9
Den Widerstand bei Wechselstrom (Sinusstrom) nennt man Scheinwiderstand (oder Impedanz). Der Scheinwiderstand einer realen Spule setzt sich aus dem Wirkwiderstand
(Widerstand des Drahtes aus dem die Spule gewickelt wurde) und dem induktiven Blindwiderstand zusammen.
Zeichne das Ersatzschaltbild einer realen Spule (Kapitel 7.3.2 Reihenschaltung
aus Wirkwiderstand und induktivem Blindwiderstand). Zeichne alle Spannungen
und Ströme ein.
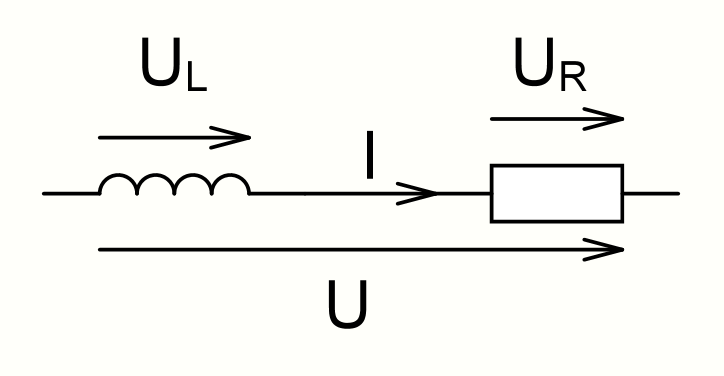
Aufgabe 10

Ergründe warum die Lampe \(L_1\) sofort leuchtet, während die Lampe \(L_2\) erst langsam zu leuchten beginnt.
Nähere Erklärungen findest du im Material von LEIFIphysik.
Antwort
Das Einschalten der Spannung ist eine schlagartige Veränderung der Spannung. Diese Veränderung der Spannung führt in der Spule zum Aufbauen eines Magnetfeldes und zeitgleich zur Selbstinduktion einer Spannung, welche den Strom reduziert. Sobald das Magnetfeld komplett aufgebaut ist und sich nicht mehr ändert verschwindet die Selbstinduktion und der untere Pfad hat keine Hemmnis dem Strom gegenüber, so daß die Lampe ebenfalls leuchtet.
Aufgabe 11
Widerstände in Reihen- oder Parallelschaltung können durch Ersatzwiderstände zusammengefasst werden. Gleiches ist mit Induktivitäten möglich.
Finde die Formeln, welche die Zusammenfassungen von Induktivitäten ermöglichen.
Lösung
Reihe:
\(L_{ges}=L_1+L_2+L_3+\ldots\)
Parallel:
\(\frac{1}{L_{ges}}=\frac{1}{L_1}+\frac{1}{L_2}+\ldots\)
Oder auch:
\(L_{ges}=\frac{1}{\frac{1}{L_1}+\frac{1}{L_2}+\ldots}\)
Für nur zwei parallele Spule gilt:
\(L_{12}=\frac{L_1\cdot L_2}{L_1+L_2}\)
Aufgabe 12
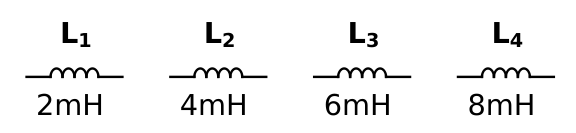
Berechne folgende Gesamtinduktivitäten \(L_\mathrm{ges}\) unter Anwendung der gefundenen Formeln:
1) \(L_1, L_2, L_3\) in Reihe
2) \(L_1,L_2,L_3\) parallel zueinander
3) \(L_4\) in Reihe mit der Parallelschaltung von \(L_1, L_2, L_3\)
Lösungen
1) \(L_1+L_2+L_3=2\ mH+4\ mH+6\ mH=12\ mH\)
2) \(\frac{1}{\frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{L_3}}=\frac{1}{\frac{1}{2\ mH}+\frac{1}{4\ mH}+\frac{1}{6\ mH}}=1,09\ mH\)
3) \(1,09\ mH + 8\ mH=9,09\ mH\)
Rückblick auf die Vermutungen
1) Der Strom bei Gleichspannung ist geringer als bei Wechselspannung.
2) Die Höhe des Stroms bleibt gleich, egal ob Gleich- oder Wechselspannung.
3) Der Strom bei Gleichspannung ist höher als bei Wechselspannung.
Lösung ist die Vermutung 3